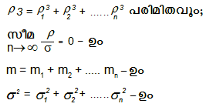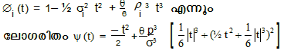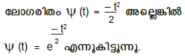This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കേന്ദ്രീയ സീമാസൂത്രം
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
കേന്ദ്രീയ സീമാസൂത്രം
Central Limit Theorem
സാംഖ്യികത്തില്‍ സ്ഥിരപ്രതിഷ്ഠ നേടിയിട്ടുള്ള ഒരു സിദ്ധാന്തം. അനാശ്രിതചരങ്ങ (indpendent variables)ളുടെ മാധ്യം (mean) ഉപഗാമി എന്ന നിലയില്‍ (asymptotically) നോര്‍മല്‍ വിതരണത്തെ അനുസരിക്കുമെന്നതാണ് ഈ സൂത്രത്തിന്റെ അന്തഃസത്ത.n അനന്തത്തിലേക്കു പ്രവണമാകുമ്പോള്‍ (n → ∞) ബൈനോമിയല്‍ വിതരണം നോര്‍മല്‍ വിതരണത്തിലേക്കു പ്രവണമാകുന്നു എന്നതാണ് ഈ പ്രമേയത്തിന്റെ പ്രതിപാദ്യം. ഇതിന്റെ സാമാന്യവത്കൃത രൂപമാണ് കേന്ദ്രീയ സീമാസൂത്രം (Central Limit Theorem).
ലിന്‍ഡിബെര്‍ജ്-ലെവി അവസ്ഥ (Lindeberg Levy condition), ലിയോപൊണോവ് അവസ്ഥ (Liapunov condition) എന്നീ രണ്ടവസ്ഥകളിലാണ് ഈ സൂത്രം തെളിയിച്ചിട്ടുള്ളത്. രണ്ടിടത്തും ഇതു സാധിച്ചിരിക്കുന്നത് മാനകീകൃത ചരത്തിന്റെ ലക്ഷണഫലനം മാനകീകൃത ചരത്തിന്റെ ലക്ഷണഫലനത്തിലേക്കു പ്രവണമാകുന്നു എന്നു കാണിച്ചുകൊണ്ടാണ്.
കേന്ദ്രീയ സീമാസൂത്രം ലിന്‍ഡിബെര്‍ജ്- ലെവി അവസ്ഥയില്‍. മാധ്യം m ഉം മാനകവിചലനം σ ഉം ആയ വിതരണത്തെ അനുസരിക്കുന്ന ചരങ്ങളാണ് X1, X2, ......... Xnഎങ്കില്‍
ഉപഗാമി എന്ന നിലയില്‍ നോര്‍മല്‍ 
ആയിരിക്കും.
ഈ പ്രമേയം തെളിയിക്കുന്നതിനുവേണ്ടി (Xi) ന്റെ ലക്ഷണഫലനം ∅ (t) എന്നു സങ്കല്പിക്കുമ്പോള്‍
ഇവയ്ക്കു പുറമേ, t സ്ഥിരമാക്കി നിര്‍ത്തി n നെ അനന്തത്തിലേക്കു പ്രവണമാക്കുമ്പോള്‍ പൂജ്യത്തിലേക്കു പ്രവണമാകുന്ന ഒരു സംഖ്യയാണ്
എന്ന് എഴുതാവുന്നതാണ്. ഇതില്‍ n അന്തത്തിലേക്കു പ്രവണമാകുമ്പോള്‍
എന്നു ലഭിക്കുന്നു. ഇത്, മാധ്യം പൂജ്യവും മാനകഫലനം 1-ഉം ആയിട്ടുള്ള നോര്‍മല്‍ വിതരണത്തിന്റെ ലക്ഷണഫലനമാകയാല്‍ ഉപഗാമി എന്ന നിലയിലുള്ള X̅-ന്റെ വിതരണം നോര്‍മല്‍
ആയിത്തീരുന്നു.
കേന്ദ്രീയ സീമാസൂത്രം ലിയോപൊണോവ് അവസ്ഥയില്‍. മാധ്യം mi,മാനവികവിചലനം σi,തൃതീയക്രമ കേന്ദ്രീയ നിരപേക്ഷ - ആഘൂര്‍ണം (absolute central moment of order three)ρ3i,/sub> ആയിട്ടുള്ള ഒരു ചരമാണ് Xi (i = 1,2,....n)എങ്കില്‍
ആയിരിക്കുമ്പോള്‍ X = X1 +X2 +......... Xn ഉപഗാമി എന്ന നിലയില്‍ നോര്‍മല്‍ (m, σ)ആയിരിക്കും.
ഇതു തെളിയ്ക്കുന്നതിനായി (Xi-mi) യുടെ ലക്ഷണഫലത്തെ ø,(t)കൊണ്ടും,ഒന്നില്‍ കവിയാത്ത നിരപേക്ഷ മൂല്യമുള്ള ഒരു സംഖ്യയെ θ കൊണ്ടും 
യുടെ ലക്ഷണഫലത്തെ ψ(t)കൊണ്ടും കുറച്ചാല്‍
എന്നും കാണാം. ഇവിടെ n അനന്തത്തിലേക്കു പ്രവണമാകുമ്പോള്‍
അതായത് X- ന്റെ വിതരണം നോര്‍മല്‍ (m,σ) ആണ് എന്നര്‍ഥം.
ഈ ഉപപത്തിയിലെ തൃതീയ ക്രമനിരപേക്ഷ ആഘൂര്‍ണങ്ങളുടെ പരിമിതത്വസങ്കല്പം അവശ്യം വേണ്ടതല്ലെന്നും ഈ പ്രമേയം ശരിയാകാന്‍ Xi-യുടെ വിതരണഫലനം Fi(x) ആയിരിക്കുമ്പോള്‍ അവശ്യം പര്യാപ്തവുമായ നിബന്ധന,
മാത്രമാണെന്നും ലിന്‍ഡിബെര്‍ജും ക്രാമറും സമര്‍ഥിച്ചിട്ടുണ്ട്.
ദ്വിതീയ-ആഘൂര്‍മം പരിമിതമല്ലാത്ത ചരങ്ങളില്‍ കേന്ദ്രീയ സീമാസൂത്രം സാര്‍ഥകമാകുന്നതല്ല. ആകയാല്‍.
എന്ന കോഷി (Cauchy) വിതരണത്തെ അനുസരിക്കുന്ന nചരങ്ങളുടെ മാധ്യത്തിന്റെ വിതരണം ഉപഗാമി എന്ന നിലയില്‍ നോര്‍മല്‍ ആയിരിക്കുന്നതല്ല. എന്നാല്‍ ഇതിനും ചില അപവാദങ്ങള്‍ (exceptions) കാണാം.
സംഭവ്യതാ സിദ്ധാന്തത്തിന്റെ പുരോഗതിയില്‍ ഗണ്യമായ പങ്ക് നിര്‍വഹിച്ചിട്ടുള്ള സൂത്രമാണ് കേന്ദ്രീയ സീമാസൂത്രം.
(ഡോ. പി. യു. സുരേന്ദ്രന്‍)
